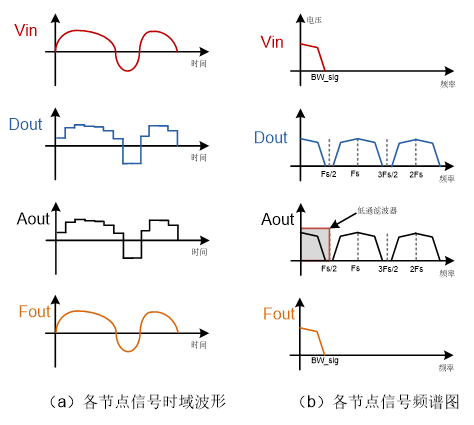
傅里叶变换是一种数学工具，它能够将时域信号（即随时间变化的信号）转换为频域信号（即随频率变化的信号），或者将频域信号转换回时域信号。这种转换关系使得我们也可以更加深入地理解和分析信号的特性。

  具体来说，时域信号是描述信号随时间变化的函数，而频域信号则是描述信号随频率变化的函数。傅里叶变换建立了时域信号和频域信号之间的桥梁，使得我们可以从频率的角度去分析时域信号。通过傅里叶变换，我们可以得到信号的频谱，即信号在不同频率下的分量及其幅值和相位信息。

  傅里叶变换在音频信号处理中发挥着至关重要的作用。以下是傅里叶变换在音频信号处理中的一些主要应用：

  通过傅里叶变换，我们可以将音频信号从时域转换到频域，从而分析信号中不同频率成分的强度和分布。

  、乐器声音分析、环境噪声监测等领域是一项基本的工具。例如，在音乐信号处理中，通过傅里叶变换我们可以分析出音乐信号的基频、谐波结构以及不同音符对应的频率分量。

  滤波器的频率响应通常通过傅里叶变换来分析和设计。利用频域滤波，我们可以更精确地控制信号的频谱特性，并提高滤波器的性能。

  中发挥了关键作用。通过分析回声的频谱特性，设计频域滤波器或自适应滤波器，可以有效减少或消除回声和混响。

  等利用了人耳对不同频率的敏感度差异，通过傅里叶变换分析音频信号的频谱，将不重要的频率分量丢弃或压缩，从而大幅降低音频文件的大小。

  在这些压缩算法中，傅里叶变换用于识别并量化音频信号的频谱成分，使得压缩后的音频在保持音质的同时极大地减少了数据量。

  STFT是傅里叶变换的扩展，适用于处理非平稳信号。它将信号分成多个短时段，并对每个时段进行傅里叶变换，从而得到信号随时间变化的频率成分。

  STFT的结果通常以语谱图的形式展示，即频率随时间的变化图。语谱图广泛应用于语音识别、音频效果分析、声源定位等领域。

  综上所述，傅里叶变换在音频信号处理中具有广泛的应用和重要的作用。它为我们提供了一种从时间域到频率域的视角，使得我们能更全面地理解和处理音频信号。

  的原因、定义、物理意义简述 /

  的详细讲解 /

  的描述，但是大都让人很难理解太过抽象，尽是一些让人看了就望而生畏的公式的罗列。 要理解

  非科班也能玩转Android应用，体验QT跨平台能力-迅为RK3568开发板

  OptiSystem与OptiSPICE的联合使用：收发机电路的眼图分析